章立てとか考えてないのでどっかで破綻するかもしれません
自作メダルゲームを作ろう!(難)
第1回でもうガッツリふるいを掛けてしまいましたが、まだ興味ある方はどうかお付き合いお願いします
第2回は設計編、思っているものを紙に表してみましょう
スタート
さて、出来る範囲で作りたいものは思い浮かんだでしょうか
どんなものを想像したかは人それぞれなのでここでどうこう言うことは出来ません、なので例を挙げつつ設計していこうと思います
FTシリーズ青抽選機

自作入門にピッタリ
何が必要かは容易に想像できるはずです
電飾やセンサーを無しにシンプルに考えるなら抽選機本体、ボール、ポケットを回すモーター、ボールを転がす傾斜の4つでしょうか、実際に作ったことは無いので憶測で語っていきます
(※他の方がどのようにしているかは一切調べずに書いています、コピーしても仕方ないというのと前例が無い場合を想定しているため)
では寸法を考えていきたいところですが…どうしましょう?
自作メダルゲームを設計をするうえで個人的におススメなのは一番寸法に自由が利かない、かつ一番大事なパーツから全体の寸法を決めるやり方です
この場合であれば抽選機かボールのどちらかの寸法を決めてしまいましょう
傾斜は何とかなるでしょうしモーターは決めたところで次に繋がらないのでこの2つを選定しました
1.抽選機から寸法を決める
抽選機の大きさが完成品の大きさになるのでイメージしやすいと思います
段ボールから作るとすれば、段ボール以上の大きさのものは作れません
(何枚も組み合わせれば良いかもしれませんが)
そうですね…

(画像引用 : http://new-pack.co.jp/nakamuraya/wp-content/themes/nakamuraya_theme/assets/images/products/80-300210200_01.jpg)
こんな画像があったのでこれを使ってみましょうか
まずポケットをくり抜く前の円を作るとしましょう
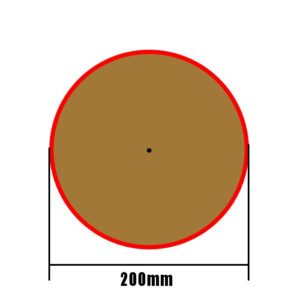
200mm x 300mm の面を使うとしたら直径200mmの円が摘出出来るかな?
ここからポケットをくり抜いたらかなり小さくなりそうですね…まあ良いか
ここからどうしましょうか、このポケットの間隔を調べてみましょうか
円周の式、習ったことはあるでしょう
(直径) x (円周率) です、円周率は厳密じゃなくても良いと思うので3.1415とします
段ボールの円周 : 200(mm) x 3.1415 = 628.3(mm)
これを12で割れば約52mm、直径200mmの円であればポケットの間隔は52mmと言うことになります
ですが実際はボールの高さを考慮する必要があるでしょう
つまりボールの中心を考慮した直径を用いて計算する必要があります
ガチ勢なら方程式立ててーってやるのかもしれませんが、ここはゴリ押しで
ボールの直径は先程の計算から52mm未満である必要があることが分かりました、なので適当にボールの直径を30mmとします
その場合、ポケットの間隔は
170(mm) x 3.1415 / 12 = 44.5(mm)
ボールサイズ30mm、ポケットサイズはボールより少し大きめに31mm、ポケット間の柵サイズは(44.5 – 31.0) = 13.5mm
ボール間の柵はボールサイズの半分と言うことになりますね、結構良い線行っているのでは?
と言うことでこの寸法で行ける…?かもしれませんね?
気になるならボールの寸法を変えて計算してみましょう
ただボールが30㎜ってラムネに入ってるあの玉かよって位小さいですね
しかも柵のサイズが1.3cmなので補強しないと段ボール程度ではふにゃっと曲がってしまうかもしれません
そもそも31mmのポケットを切り抜くのはちょっと難しいかも?
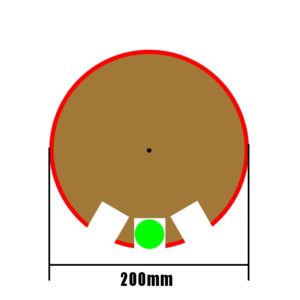
(図では面倒だったのでポケットを四角に切り抜いたため柵が異様に細くなっていますが、円形に切り抜けばもう少し余裕は出来ます)
まあ物は試しです、こういう時は試作してみましょう
今回は完成形も段ボールなのですが、実際は修正不可の金属やアクリルで作成する可能性があります
一発勝負でミスが発覚するともう終わりなので、予め加工しやすい素材で試作するのはおすすめです、自作銀河でも試作機…と言うか失敗作はあります
結果として出来そうならこの寸法で良いだろうということが分かります
もしダメだと思ったら段ボールの寸法からもう1度計算しなおします、エクセル等で数値を自在に変えられるようにしておくと便利かな
純粋にこれまでの寸法を倍にしたら段ボール直径400mm、ボール50mm~60mmで良いかな、と言う推測も出来ます
これならガチャガチャカプセルを使えば案外いい線行きそうですね?
2.ボールから寸法を決める
と言っても先程の逆順を辿るだけです
手に入りそうなボールのサイズと、柵のサイズから段ボールの寸法が決まります
その段ボールが入手出来そうならクリア!
とりあえず制作に取り掛かることが出来るだろう、ということが分かります

モーターは後から突き刺せば何とかなるでしょうし、傾斜も後付けで何とかなるのでこれでFTの抽選機は作れそうです
ぶっちゃけこれ書いてる時点で結構大変でした…FT抽選機が簡単とか言ってすみませんでした
しかも抽選機って言ってもポケットと言うよりボールが通過する穴なので本当にシンプルを突き詰めたものになるでしょう…
で
自作銀河の場合は

まず実機を観察しました
求めたかったのはボールとドームの大きさの比率です
(ドームサイズ / ボールサイズ = ?)
これを求めて、
ボールのサイズを決定してから必要となるドームの直径を求めようとしたわけですね
うん、やり方は悪くないと思います

と言うことで色々計算していけると思ったのでボールを購入
最初は実機通りの柔らかくてバウンドするボールにしたかったのですがどうしても小型のものが無かったので、amazonで跳ねそうなゴルフ練習ボールをチョイスしました
ボール直径45mmで、ドームサイズは450mmでしょう
450mmの球体なんてどう作るつもりだったんだよオラァン!?
ここ大ポカポイントです、450㎜の球体は少なくとも検索した限り存在しません
なので自作しようと思ったんですよね、透明な球体を
自分の能力過信しすぎです…
結果として大失敗に終わりました、ボールの寸法からやり直しと言うかドームの寸法から全部決めることになりました
だから重要かつ手に入る寸法が限られるものから寸法を決めろって言いたいわけです
あと出来る範囲でやらなきゃダメ
まあもっと言えばボールとドームの比率が10ってのは小さいと思います、15くらいじゃないかなあ
でも完成品のボールが30㎜、ドームが330㎜なので結果として大して変わってないんですけど

あのゲーセンでよくあるリングと寸法が素晴らしくピッタリだったのでこりゃ良いと思っていたのですが…
まあ失敗して経験を得たからこそ完成出来たわけです、挑戦としてはいい経験でした
今回のまとめ
・寸法は一番自由が利かない・重要なものを基準に決めていこう!
・書いた設計図は最後の最後まで役立つ!
・本当に実現可能かよーーーく考えよう!
…自作銀河、本当に最初は雑な思い付きで作り始めてしまいました
その結果色々無駄にしてモチベが消失したからこそ前章のあの言いっぷりなわけです


自作メダルゲームでもなんでも、作り上げた後の達成感はすごいんですけど、僕の場合コレジャナイ感が一週間後くらいに襲ってきます。
でもそういう時に限って修正しようとしたら(大)惨事になります…分かる人いるかな
マジカルシューターで1,000枚増えました…魔王が何か死んだ…
友達(メダゲー初心者)とボーナスゲームで連打すんのタノシー!ワー!って収支度外視して楽しんでたらトントン拍子で鍵揃って魔王選ばれて7連鎖して勝ちましたよええ、多分友達の運がすごかった
ボーナスゲームが全部連打すれば何とかなるのだったら人気でたんやろなぁって思いました
セミとカナブンはどっちも窓でコツコツ当たってくるから嫌いなんですけど、これも誰か分かってくれる人いませんかねぇ
セミなんか特によく窓の近くでひっくり返ってるからぶつかりすぎて死んだかと思って近づいたが最期、奇声(?)発しやがってこっちがひっくり返ることになるから嫌い
でも蝉時雨は好き、もう鳴き声だけの概念とかしないかなぁ、セミ
あーこれ分かります…直したいんですけど直せるような作りじゃないからどうにもならないっていう
自作銀河も直したい部分が多々あるのですがどうにもならず、起動が面倒なせいで全然触ってないんですよね
接着剤は便利だけど修正効かないのが痛いです
ボーナス連打でOKなら多分ここまでハマってないかなあ
技術介入だいしゅき人間なのでバッリバリの技術介入のあるゲームが好みでございます
…まあ一般的には運でどうにかするゲームの方がウケるんでしょうけど、全てのゲームが運ゲーだったら個人的には嫌ですね
せめてアウト避けるとかポケットを狙うとか、やって当然のことはやってほしいと思うんです
連打してわけわかんねーつまんねで終わるのは流石にゲームの方が可哀そうになる
わかんない(無常)
そのセミファイナルって奴も私は遭遇したこと無いんですよね
セミ自体は殺虫剤撒いたろかって思った記憶があるのでそれなりに居るはずなんですけど姿を全然見ない…
つまり私にとってセミは概念みたいなもんです
ひえっ…
こんなの作れるのかなぁ
まず円を切り抜く時点で終わりそうw
これは難しそう(小並感)
マジカルシューターって今考えるとトレイ横のセンサー部分って玉詰まらないですよね。(詰まる時は詰まるだろうけど)
(自作マジカルシューターを作るなら)沢山ボールを流す以上、詰まらないように作るのが難しそうです
ボールは手動で上に溜めてそっから出てくるようにすれば良さそう (適当
船中にに玉切れしてステップ落としそう
ビー玉+釘だと音が凄そう… 色ついてる+沢山手に入りやすい だとビー玉が綺麗で安く手に入るけどどうなんですかね
最近氷山が遊べる店舗が無くなってきて(撤去 or 100円専用)、預けがある店舗で唯一の氷山との相性が無茶苦茶悪くて泣きそうです
(1段目があまり安定しないorほぼ狙えないstしかない)とりあえずBRがしたいので突っ込みまくってたら2時間-4000 BR無し。+ 3時間-7000 BR無し。40球ぐらい抽選してるんですが… 最近山系との相性が全体的に悪い… モンハンとの相性は相変わらず抜群です。何故なのか
LvがカンストしてXPが貰えないなら鳥用に各色特攻epassを作ってはどうでしょう。そこまでする価値があるかは知りませんが…
氷山の3段目はBRポケットがサテから見て
右奥に来た位置から減速が始まるので、
傾斜やボールの転がり具合によっては
かなりBRへ行きにくいサテも存在すると思います。
毎回同じポケットに入賞してしまうようなら
店にクレーム入れた方が良いと思います。
前者の時から台が移動してたので、3段目のクセを見つつそれを踏まえて途中で隣と反対のstに移動してるんですよ… (癖が悪いと思ったら他の人がBR入った台に移動した)
再加速まで粘るかどうかぐらいの傾きなので、気持ち入りやすい~入りにくいぐらいだとは思います。BR入る1秒前に加速したり… あるあるですな
やってない1つのstが良かったのか、ただ単に運が悪いのか分かりませんが。
こういうことっすか
まあこれだけやってきてこの1回しか詰まったことが無いので極々稀ってところです
ビー玉は跳ねないしあれだけぶつけると割れかねないのでちょっと…あと重いし
特攻epassと言っても現状クリスマス装備は手に入らないのでLv72まで必死に上げないと駄目なんですよ、それで1.1倍
だったらメインのレコード伸ばしますね…
画像の上2球だけで詰まる事無くない…? というかJP演出であれだけ玉出して詰まらないんだからすごい
跳ねないといけないのか。小さめで跳ねて軽い物で摩擦少なめ、か。
実機のボール買おう!…..
(5BETスロが絶好調だったstに置いた青羽残ってたから50BETスロしたら内部爆発しててステップ事故無しで40000増えたのは草。森6面コンプとか4面コンプx2とかしたから増えたってだけだけど)
自分が作るならガリレオのクルーンかなぁ
あの絶妙のクルッ、スポッ加減を再現できたら気持ち良さそう
メダベルさんも昔ちっこいの作ってましたね
元ホームが再開店しました
in マーブル アニマ モンハン トレジャーシュート マリコロ マリチャレ バベル他
out 火山 氷山 シャドプリ
筐体増えすぎてて草、今まで行ったことのあるゲーセンで一番すごいってなぐらいの店に
個人的には大黒柱シャドプリがお亡くなりになったのがほんと悲しい、トレジャーシュートなんかいらないからカエシテ・・・
シャドプリが消えたとなるとわたしの技量ではマジカルで勝つ以外預けつくれない(勝てるとは言ってない)
真剣に1ベットタイムかなぁ
昔作った奴は雑の雑でしたけど思った以上に良い動きしてくれたので、適当に穴開けるだけでも案外出来るのかもしれないです
まあ微妙な傾斜と穴をどう作るかが問題ですが…
筐体が多いに越したことは無いですがだからと言って何でもあれば良いって訳じゃあないんですよね
ぶっちゃけバベルとか私的には置物
マジカルに貢ぐための資金作りが出来る機種とド本命マジカルシューターが生き残っていればもうそれだけで生きていけるんですが
中々都合よくはいかないもんですね…
(非常食はガチ破産した時につまみたい、普段から無いものとして遊んだほうが現金的には大変優しいです
一回破産すれば冷静になれるはず)